NIOSH Lifting Equation - Assessing Relevant Handling Factor
On this page
- Is there a way to know if a lift is too heavy?
- What do you have to know to calculate the recommended weight limit (RWL)?
- How do I figure out which multiplier value to use?
- Where can I find more information about these factors?
- Can I use this equation in all situations?
- So, when do I use this equation?
- Where can I get more information about the Revised NIOSH lifting equation?
- Why is this equation called "revised"?
Is there a way to know if a lift is too heavy?
Back to topThe following recommendations are based on the "Revised NIOSH equation for the design and evaluation of manual lifting tasks" (NIOSH is the National Institute for Occupational Safety and Health in the United States).
The NIOSH lifting equation takes into account the weight plus several other variables in lifting tasks that contribute to the risk of injury. For example, if the situation requires frequent lifts or lifting loads far away from the body, there is an increased risk of injury. Under these conditions, the weight limit would be reduced from a baseline weight or "load constant" (LC) to a recommended weight limit (RWL). A "load constant" (LC) of 23 kg (about 51 lb) was established by NIOSH as a load that, under ideal conditions, is safe for 75% of females and 90% of males.
The recommended weight limit is calculated by using the NIOSH lifting equation.
What do you have to know to calculate the recommended weight limit (RWL)?
Back to topFirst, you have to measure or assess several variables related to the lifting task. The six variables that are considered in determining the recommended weight limit (RWL) are:
- the horizontal distance (H) the load is lifted (distance of hands from midpoint between ankles),
- the starting height of the hands from the ground, (vertical location, V),
- the vertical distance of lifting (D),
- the time between lifts or frequency of lifting (F),
- the angle of the load in relation to the body (e.g., straight in front of you or off to the side, A), and
- the quality of the grasp or handhold based on the type of handles available (hand-to-load coupling, C).
Each of these variables is then assigned a numerical value (multiplier factor) from look-up charts. The NIOSH equation includes six multiplier factors to calculate the recommended weight limit (RWL):
where LC is the load constant and other factors in the equation are:
- HM, the Horizontal Multiplier factor,
- VM, the Vertical Multiplier factor,
- DM, the Distance Multiplier factor,
- FM, the Frequency Multiplier factor,
- AM, the Asymmetric Multiplier factor, and
- CM, the Coupling Multiplier factor.
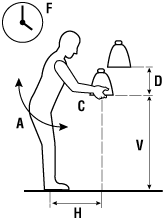
Figure 1: F=Frequency, A=Angle of load, H=Horizontal, C=Coupling, D=Distance travelled, V=Vertical location
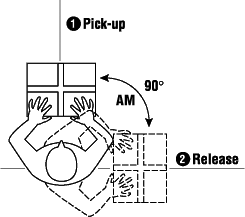
Figure 2: AM=Asymmetric Multiplier, the angle of the body in relation to the load
The closer the multiplier factors are to 1, the better the conditions are for a Recommended Weight Limit (RWL) close to 23kg (or about 51 lbs). When the conditions are not within the recommended ranges, (multiplier factor farther from 1), the weight limit must be reduced accordingly.
How do I figure out which multiplier value to use?
Back to topTo figure out which multiplier value to use, you must measure the distance in centimetres for each factor. For example, to determine horizontal multiplier, measure the distance from in between the person's ankles to their hands when holding the object. Write down this number. Next, look up the number on the "horizontal distance" chart (see Calculating Recommended Weight Limit (RWL)) and find the matching multiplier factor. Use this factor in the lifting equation. NIOSH does allow for extrapolation for values that do not match the figures presented in their tables, or you can opt to use the next higher value (more protective) from the table.
Do the same for the other five factors.
- Vertical Multiplier is the distance is measured as the starting point of the lift and is the distance of the hands up from the ground. Measure this distance and use the number to determine which value to use on the chart (see Calculation Recommended Weight Limit).
- Distance Multiplier is the number of centimetres the load travels up (or down) from the starting position. Again, measure this distance and use the number to determine which value to use on the chart (see Calculation Recommended Weight Limit).
- Frequency Multiplier is how often the lift is repeated within a certain time period. You need to determine if the lift is done while standing or stooping, for more or less than one hour (in total time for the shift), and how much time there is for rest between lifts.
- Asymmetric Multiplier measures if the body must twist or turn during the lift. This measurement is done in degrees (with 360 being one complete circle).
- Coupling multiplier determines the "coupling" or type of grasp the person has on the container. It rates the type of handles as good (handles), fair (make-shift cut outs in cardboard boxes) or poor. You also need to know if the lift is done in a standing or stooping position.
Once you have all these values, you can use the Revised lifting equation calculator to determine a recommended weight limit.
Compare this value with the actual weight of the object. If the recommended weight limit is lower than the actual object, you will have to determine which factor(s) is contributing the highest risk and modify the lift. (The factors that are contributing the highest risk will have the lowest multiplier values).
Where can I find more information about these factors?
Back to topOther OSH Answers documents in this section for examples which show how to use this information and to reduce the risk of injury:
Can I use this equation in all situations?
Back to topNo. The Revised NIOSH Lifting equation only applies in certain situations. It does not apply in situations where a person is lifting (or lowering):
- with one hand,
- for over 8 hours,
- while seated or kneeling,
- in a restricted work space,
- objects that are unstable (such as buckets or containers of liquids),
- while pushing or pulling,
- with wheelbarrows or shovels,
- with high speed motion (faster than about 0.76m/s (or 30 inches/second),
- extremely hot or cold objects or in extreme temperatures, or
- with poor foot/floor coupling (high risk of a slip or fall).
So, when do I use this equation?
Back to topThis recommendation applies to most workers for:
- two-handed lifting,
- comfortable lifting postures, and
- comfortable environments and non-slip floorings.
Calculation of recommended lifting limit using this formula indicates which of the six components of the task contribute most to the risk. The lower the multiplier factor, the more it contributes to the risk.
Where can I get more information about the Revised NIOSH lifting equation?
Back to topThe NIOSH document Applications Manual For the Revised NIOSH Lifting Equation is available on the Internet. This document explains which situations in which the equations does and does not apply, as well as more information and details. This document should be consulted before applying weight limits in a workplace.
Why is this equation called "revised"?
Back to topNIOSH published their first lifting equation in 1981. In 1994, a new "revised" equation was published which took into account new research findings and other variables that were not used in the first equation. This "revised" equation can be used in a wider range of lifting situations than the first equation.
- Fact sheet confirmed current: 2016-07-04
- Fact sheet last revised: 2021-04-27

